Will getting a new heat pump save you money in the long run?

Traditionally, heat pumps were a swell answer in the south and western U.S, where they've been kickin' hard since the 1970s.  After all, they provide both heating in the winter, and, more importantly for much of this region, air conditioning in the summer.  They obviated the need to deal with a natural gas hookups or their concomitant greatly-fluctuating utility bill.   But now, there's a big push toward energy-efficient heat pumps that can run in colder (northern) weather.  The Biden administration, via their Inflation Reduction Act, is hoping to blanket (pun intended) these regions with these units so as to avoid burning fossil fuels (most commonly natural gas, so this posting will focus on that).  The Day 1 discounts are huge:  Get 30% off on any EnergyStar-rated heat pump, and possibly also get some cash-back rebate money (depending on your location and your financial need) to discount both the purchase and the install of these critters.  So far, so good.  But when is it worthwhile, and when might you be myopic in your decision to latch on to a heat pump, later regretting the high ensuing electric bills?  Well, you need to put the math to it based on your individual circumstances, and we're here to help.

If you're new to heat pumps, the concept initially is pretty foreign compared to a gas furnace: burn something and feel warm.  How can an electric device possibly be more efficient or more economical than that? Well, their efficiency, and potential savings, comes from the fact that heat is carried from the outside (where it's just sitting around doing a lot of nothing) to the inside of your home.  What?  It's 18 degrees outside!  There's no heat out there!  In fact, there is, it's all relative, Einstein.  And that heat is enhanced when the refrigerant that's carrying it is compress and later changed from a gas to a liquid inside of the coil as cold air in your house runs over it.  This cooler refrigerant is then expanded at the outside unit part of the heat pump, and that outdoor unit then becomes super cold as part of the refrigeration cycle and picks up the outdoor heat once again and the process repeats.  How this all works is maybe half as hard to get one's brain around as imagining the universe going on forever.  But in short, think of yourself as a heat pump when you put your arm through your car window and into the Burger King drive-thru window to fetch a 677-calorie Whopper.  You exerted maybe 1/4 calorie to do that?  And, well, maybe you had to respond to some emails or sit through a meeting for a few minutes to get the $5 to pay for it.  Okay, another 20 calories.  Still, 677 calories back for a 20.5 calorie investment, not bad (unless you're on a diet). This is how heat pumps work, and why the efficiency can be more than 1.  They carry more BTUs in than they need to run.  So, yes, it may be possible for heat pumps to win.

Next, what's going on with rates?  Natural gas has been cheap in recent years, but with war going on in Europe straining supplies just as the economy is recovering, prices are up almost 50% over last year at this time. And, so there's greater fluctuation in these rates than the rates of electricity, but still, since 38% of electricity is generated from natural gas (https://www.eia.gov/tools/faqs/faq.php?id=427&t=3), electric rates are closely correlated to gas rates and are also rising.  So, the decision is even more mor important now than when rates where cheaper.

In your own analysis, you're going to need a few things, and we'll throw these same things, with different values, into the analysis for a house in Michigan.  The things need are...

1.  What's the efficiency of your old gas furnace?  This is simply a percentage of BTUs delivered to the space vs. BTUs burned.  Average Fuel Utilization Efficiency (AFUE) is the term for this.  From 1987 to 2007, the required efficiency needed to be 78%.  Since then, it's needed to be 80%.  If your furnace is old than this (and if you have an older home, quite likely it is, since furnaces are simpler than air conditioners to maintain and to keep running), it may be only 60% efficient.  Assume this value for our example.

2.  Alternatively, what's the efficiency of the furnace you'd put in if you were to replace this one instead of get a heat pump?  Hint:  Newer efficient models are 90% efficient.  Yes, these models are more expensive.  So, the Day 1 cost for this must also be taken into account vs. getting a new heat pump or doing nothing in terms of changes.  Anyway, we'll use this value to see if this beats what a new heat pump could deliver in terms of savings on a monthly basis.

3.  What's the efficiency of the heat pump you're looking at getting?  For the heat pump to be eligible for rebates and tax credits after then end of 2022, the efficiency must have a Heating Seasonal Performance Factor (HSPF, calculated as BTUs delivered/watt-hours consumed) of at least 8.1 BTUs/watt-hours.  Since a watt-hour is 3.41 BTUs, that means that the efficiency in watt-hours out vs. watt-hours in needs to be (8.1 BTUs/watt-hour)* (1 watt-hour/3.41 BTUs) = 2.38 watt-hours out for every watt-hour put into running the heat pump.  So, pretty efficient.  (By the way, air conditioners, or heat pumps running in air condition mode, need to be 4.46 watt-hours out vs. watt-hours in.  Why can (and must, for EnergyStar rating) a heat pump be so much more efficient in cooling?  Well, remember, the temperature difference from, say 97 degrees, down to 77 degrees is not as big a jump as from 17 degrees to 77 degrees.  So, the heat pump needs to work harder and is less efficient in heating to achieve this temperature difference. )

 4.  What's your price for natural gas?  Usually, natural gas is billed in Mcf (1,000 cubic feet).  1 Mcf = 1,037,000 BTUs.  This is a used approximation, and will vary depending on the density of the gas, but it's accepted.  And, on some bills, add up the variable elements of the bill for the Mcf.  That is, in Michigan, for instance, there's a value for gas distribution of $5.18/Mcf and a value for gas cost recovery (a bizarre term meaning that the utility need to refill their supply, or recover that supply, for the amount you burn, but it's really the amount you burn, or consume) of $7.43/Mcf.  Add these two together and get a recent high price of $12.61/Mcf.

5.  What's your price of electricity?  In Michigan, it's currently $.1713/kWh. 

In our Michigan example, the Mcf burned looks like this.  You can run this same example from your natural gas bill.

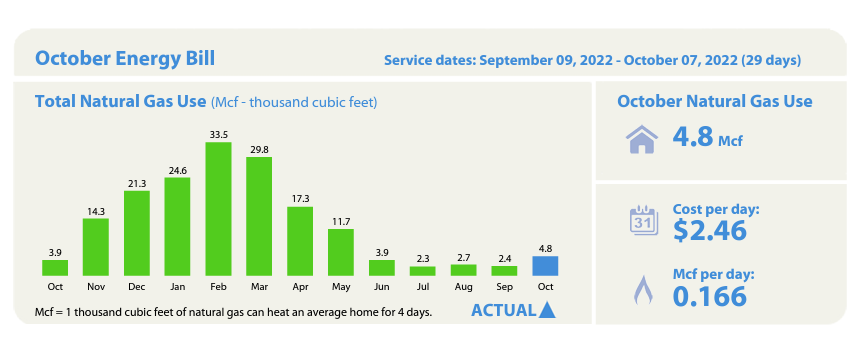
How much of this gas is actually used for air heating vs. water heating?  It looks like in the summer, when there's only hot water demand but no heat demand, around 2.5 Mcf are still used for that, so subtract off 2.5 to get the Mcf used for heating...

 

Running with gas	Billed Mcf	To get air heating Mcf, subtract
		off the water heating, which
		looks to be around…
		2.5
October	3.9	1.4
November	14.3	11.8
December	21.3	18.8
January	24.6	22.1
February	33.5	31
March	29.8	27.3
April	17.3	14.8
May	11.7	9.2
June	3.9	1.4

 

Multiply this right-hand column by the $12.61 rate from '4' above to get these base...

 

Running with gas	Billed Mcf	To get air heating Mcf, subtract	To get heating $, assume
		off the water heating, which	$/Mcf is…
		looks to be around…	12.61
		2.5
October	3.9	1.4	17.65
November	14.3	11.8	148.80
December	21.3	18.8	237.07
January	24.6	22.1	278.68
February	33.5	31	390.91
March	29.8	27.3	344.25
April	17.3	14.8	186.63
May	11.7	9.2	116.01
June	3.9	1.4	17.65
			$1,737.66

 

But, remember, when we're talking heating and cooling, we're normally talking BTUs, so let's convert to BTUs, and then to delivered BTUs, which is only 60%, in this example, of burned BTUs, since 40% are going 'up the smoke stack' since this unit in the example is very old...

 

Running with gas	Billed Mcf	To get air heating Mcf, subtract	To get heating $, assume	Burned BTUs	The percentage of BTUs delivered are
		off the water heating, which	$/Mcf is…	(1 Mcf = 1,020,000.163 BTUs)	less than those burned.  The ratio is…
		looks to be around…	12.61		0.6
		2.5
October	3.9	1.4	17.65	1,428,000	856,800
November	14.3	11.8	148.80	12,036,002	7,221,601
December	21.3	18.8	237.07	19,176,003	11,505,602
January	24.6	22.1	278.68	22,542,004	13,525,202
February	33.5	31	390.91	31,620,005	18,972,003
March	29.8	27.3	344.25	27,846,004	16,707,603
April	17.3	14.8	186.63	15,096,002	9,057,601
May	11.7	9.2	116.01	9,384,001	5,630,401
June	3.9	1.4	17.65	1,428,000	856,800

 

Delivered BTUs is what we need for learning what a heat pump needs to deliver.  No smoke stack with a heat pump.  So, we'll work with the delivered BTUs in the above right to eventually convert to kWh (kilowatt-hours), the billing metric for the electricity used by heat pumps.  First, we need to convert from BTUs to Wh (watt-hours), since the efficiency of the heat pump we're working with is assumed to be 8.1.  So BTUs/month divided by BTUs/watt-hour gives watt-hours/month...

 

Running with hp	Delivered	To get Whs/month, assume BTU/watt-hours is…
	BTUs	8.1
October	856,800	105,778
November	7,221,601	891,556
December	11,505,602	1,420,445
January	13,525,202	1,669,778
February	18,972,003	2,342,223
March	16,707,603	2,062,667
April	9,057,601	1,118,222
May	5,630,401	695,111
June	856,800	105,778

 

To get kW-h/month (kilowatt-hours/month), we simply need to divide the right-hand column by 1,000...

 

			kW-h/month is
Running with hp	Delivered	To get W-hs/month, assume BTU/watt-hours is…	W-hs/month divided
	BTUs	8.1	by 1,000
October	856,800	105,778	105.78
November	7,221,601	891,556	891.56
December	11,505,602	1,420,445	1,420.44
January	13,525,202	1,669,778	1,669.78
February	18,972,003	2,342,223	2,342.22
March	16,707,603	2,062,667	2,062.67
April	9,057,601	1,118,222	1,118.22
May	5,630,401	695,111	695.11
June	856,800	105,778	105.78

 

How much does a kilowatt-hour cost?  We're assuming $.1713 in MI.  Use this table here in Q3 to check your area..https://airspool.com/seercalculator.  So, 

kilowatt-hours/month x $.1713/kilowatt-hour give this monthly amount...

 

Running with hp	Delivered	To get Whs/month, assume BTU/watt-hours is…	Whs/month divided	assume $/kWh is…
	BTUs	8.1	by 1,000	0.1713
October	856,800	105,778	105.78	18.12
November	7,221,601	891,556	891.56	152.72
December	11,505,602	1,420,445	1,420.44	243.32
January	13,525,202	1,669,778	1,669.78	286.03
February	18,972,003	2,342,223	2,342.22	401.22
March	16,707,603	2,062,667	2,062.67	353.33
April	9,057,601	1,118,222	1,118.22	191.55
May	5,630,401	695,111	695.11	119.07
June	856,800	105,778	105.78	18.12
				$1,783.50

 

Conclusion:  For heating with gas with this old inefficient unit, it costs, currently, around $1,737.66/winter.  And, for heating with an efficient heat pump, it costs, currently, around $1,783.50.  So, to pay an extra $45.84/winter, it may not be very motivational to switch to a heat pump.  But, a couple of caveats...

1.  This heat pump is the minimum efficiency to be certified by EnergyStar to be energy efficient.  If you can find one with an HSPF of 12 or higher, the math looks very different, saving you $533.80/winter.

 

			kW-h/month is	To get to $/month,
Running with hp	Delivered	To get Whs/month, assume BTU/watt-hours is…	Whs/month divided	assume $/kWh is…
	BTUs	12	by 1,000	0.1713
October	856,800	71,400	71.40	12.23
November	7,221,601	601,800	601.80	103.09
December	11,505,602	958,800	958.80	164.24
January	13,525,202	1,127,100	1,127.10	193.07
February	18,972,003	1,581,000	1,581.00	270.83
March	16,707,603	1,392,300	1,392.30	238.50
April	9,057,601	754,800	754.80	129.30
May	5,630,401	469,200	469.20	80.37
June	856,800	71,400	71.40	12.23
				1,203.86

 

2.  You need to have the BTUs for your coldest day if you're going to run with heat pump only.  In the above example, our peat BTU load (for delivered BTUs) was 18,972,003 for the February billing (so, these BTUs were probably used in January).  Assuming, first, that each of these BTUs was used consistently each hour of the month, then 18,972,003 BTU/month x 1 month/31 days x 1 day/24 hour gives 25,500 BTUs/hour, or ~ 2 tons of heating.  But realistically, much more of this heat is being used in the early morning, when it's still dark and at its coldest, than at 3pm in the afternoon when there's light coming through the windows and it's a bit warmer outside.  Will a 5-ton unit hold the house?  Probably.  If not, you may need to get another unit, since 6-ton units are not a normal size in residential heating and cooling.  But keep in mind that a 5-ton unit may be too big in the summertime, and, unless the unit is variable speed (hopefully it is if it's listing high efficiency), the unit may continue to cycle on and off in the summer, and may make you feel uncomfortable.

3.  The efficiency in the above example is averaged out to be 8.1 HSPF.  That's testing over a range of temperatures.  That can be good news or bad news.  In January, the unit's not going to be at 8.1 HSPF.  So, you'll be paying more per BTU then.  But, the flip side is that the BTUs in the early spring or late fall will be very inexpensive compared to running your furnace.  Why?  Because the compressor of the heat pump needs to work really hard when it's super cold, and doesn't need to work hard at all if it's, say, 45 degrees Fahrenheit outside.  So, another idea is to get a smaller heat pump (e.g., a mini split) to nip away much of your winter heating load for a much lower $/btu figure than running the big heater all winter long.

Oh, we need to finally circle back and look at what a super-efficiency (from '2' above, 90% efficiency) new furnace would cost to heat. The easiest way to do that is simply take what was spent on heating before, and multiply it by the fraction of (old unit efficiency/new unit efficiency).  From '1' and '2' above, we have .6 for the old unit and .9 for the new unit.  So, multiply the old spend by .6/.9, or .667.  This gives...

60% efficient	90% efficient
17.65	11.77
148.80	99.20
237.07	158.05
278.68	185.79
390.91	260.61
344.25	229.50
186.63	124.42
116.01	77.34
17.65	11.77
$1,737.66	$1,158.44

 

Of course, there's no tax incentives or rebates for one of these to cover the Day 1 cost, but, Day 1 cost and environment (and your grandkid's healthy future) aside, a super-efficient new furnace looks pretty good, with a projected savings of $579.22/year.  Currently, it's around $1,737.66/winter with the old inefficient unit, and it would be only around $1,158.44 with a new efficient unit.